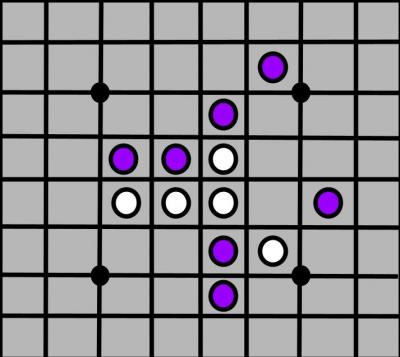
Reversi on graphs: Reversi is a two-player game, typically played on an 8x8 grid with 64 two-sided disks.  Players take turns laying disks on the board, surrounding the opponent's disks in order to convert the disks to their own.  The player with the most disks once all legal moves have been played wins the game.  We look at extending this game to different graphs (essentially changing the game board).

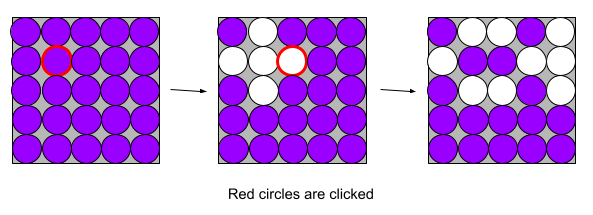
Lights out on surfaces: Lights out is a single-player electronic game, played on a 5x5 grid.  The game begins with an initial configuration of lights which the player must turn off.  The complication is that each change to a light state affects the state of all of the neighboring lights.  We look at the game after we glue and twist the grid or allow for more light states.

.

The Hochschild cohomology of an associative algebra is a Gerstenhaber algebra, having a graded ring structure given by the cup product and a compatible graded Lie algebra structure given by the Gerstenhaber bracket. The cup product can be defined generally from multiple perspectives and has been studied for many classes of algebras. The Gerstenhaber bracket, however, has not admitted such a general definition, making computations difficult. In this dissertation, we characterize the Gerstenhaber algebra structure on the Hochschild cohomology of group extensions of quantum complete intersections. We utilize the notion of twisted tensor products, a noncommutative tensor product, and adapt a technique of Wambst’s to compute the graded ring structure on Hochschild cohomology. The bracket structure is computed by employing an alternative description given in recent work of Negron and Witherspoon. When the group is trivial, this work extends the previous computations of the graded ring structure of Hochschild cohomology of quantum complete intersections to include the bracket structure. As an example, we compute the Gerstenhaber algebra structure for two generator quantum complete intersections extended by selected groups.